Contents |
The Element data window can most conveniently be viewed by pressing F5 (Window : Layout : Warrior layout). When you double-click the element data window, you can view the element's repetition history.
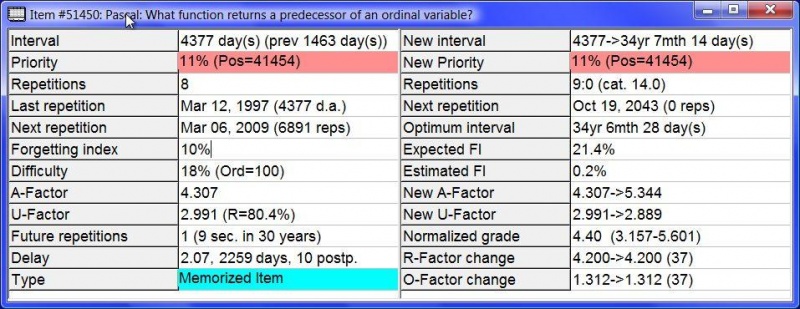
This is a typical element data window after a repetition:
In the presented example, the element is listed at position #51450 in the collection and its title is "Pascal: What function returns a predecessor of an ordinal variable?". Element titles are automatically generated from the first question text.
Element data (left panel)
Element data is displayed in the left panel of the element data window. It includes the following fields:
- Interval - current interval of the item (i.e. the number of days between Last repetition and Next repetition), and the previous interval in days (in parentheses). Here the item has last been repeated in 1997 (8th repetition) and the interval since then was 4377 days (almost 12 years). The interval between the 7th and 8th repetition was 1463 days (over 4 years). Important! If you advance a repetition, its interval and U-Factor will both be corrected for spacing effect. Consequently, the previous interval field here will point to an earlier date than the actual date of the repetition. This earlier date will equal the date on which the repetition would have to have been made in the optimum schedule to produce the approximately same combination of memory stability and retrievability as the actually executed advanced repetition. This virtual repetition date will come earlier than the date of the advanced repetition, but later than the date of the preceding repetition. For more see: Algorithm SM-15
- Priority - priority of the element in percent and as a position in the priority queue. This field is color-coded. Elements with the highest priority are red, while elements of the lowest priority are white. The item in the picture has a priority of 11%. This means that only 11% of elements have a higher priority. The item sits on the position 41454 in the priority queue. This means that 41453 elements in the collection have a higher priority. Because of the relatively high priority (i.e. low percent value), this field has a pinkish hue.
- Repetitions - number of repetitions of the displayed element. If the element had been forgotten, the number of memory lapses is displayed in parentheses. Once the element is forgotten, the count of repetitions begins from scratch (i.e. Repetitions equals 1 again). In the example presented in the figure, the item has been repeated 8 times and has not been forgotten yet. As the picture was taken immediately after the 8th repetition, the field will be updated as soon as the repetition data panel on the right is cleared. It will change from 8 to 9
- Last repetition - date of the last repetition of the item. This field will also inform you how many days have passed since the last repetition ("d.a." stands for "days ago"). Here the 8th repetition took place on Mar 12, 1997 and the current repetition which has just taken place is recorded as executed on Mar 06, 2009. The 8th repetition took place 4377 days ago, i.e. exactly as indicated by Interval (these two numbers are the same on the day of the repetition on condition the repetition is not executed with delay)
- Next repetition - date on which the next repetition of the item should take place, and the number of elements scheduled for repetition on that particular day. If the displayed element belongs to outstanding queue (i.e. it is scheduled for repetition for today), the latter will be replaced with its priority expressed as position in the outstanding queue. Next repetition of this item should take place on Mar 06, 2009 and it has actually just been made. The 10th repetition has been scheduled to take place on Oct 19, 2043 as indicated in the one row up in the repetition data panel on the right. The presented item is only one of 6891 elements scheduled for review on Mar 06, 2009. This high number indicates either a longer break in learning or a heavily overloaded learning process, which may be a norm in incremental reading
- Forgetting index - allowed probability of forgetting the item in each repetition (in percent). Forgetting index can be changed to a desired value (e.g. with Ctrl+Shift+P via Element parameters or by changing it in the element data window as shown in the picture). If the forgetting index is 10%, you stand a 90% chance that you will remember the item during the optimally scheduled repetition. The probability of forgetting will increase if you delay a repetition. Here the forgetting index has been set at the default 10%. See also: Forgetting index
- Difficulty - difficulty of the displayed item estimated on the basis of the following parameters: Interval, Lapses, Repetitions, A-Factor, and First grade. This field also displays element's ordinal (in parentheses). The theoretical minimum for the difficulty is 0% and the theoretical maximum is 100%. This number decreases gradually with successful repetitions or increases with memory lapses. In a typical collection, the difficulty of items usually ranges from 16% to 64%. If the difficulty reaches beyond 65% you should have a closer look at the formulation of the item (e.g. memory interference, ambiguity, excessive wording, complex answer, etc.). The presented item is estimated to be at 18% difficulty which indicates it is relatively easy to remember. See also: 20 rules of formulating knowledge
- A-Factor - A-Factor associated with the currently displayed element. A-Factor is a rough measure of item difficulty and a measure of the rate at which inter-repetition intervals increase. The higher the A-Factor, the faster the increase in intervals. For items, the most difficult items have A-Factor equal to 1.2. For tasks and topics, A-Factors equal the increase in interval in a single review and may be as low as 1.01. Note that Difficulty (above) is much more an accurate measure of item difficulty (as perceived by the user). A-Factor of 4.307 in the picture indicates that the item is relatively easy to remember
- U-Factor - U-Factor and the current estimation of element's retrievability. U-Factor is the quotient of the previous interval and the next interval. In items that have been repeated only once, U-Factor equals the first interval (in days). U-Factors make up an important element of SuperMemo Algorithm. If you do not know the algorithm, U-Factors do not have much meaning to you. Retrievability corresponds with the probability of correct recall of the item at a given point in time. Theoretically, retrievability should decline exponentially from 100% on the day of the last repetition, to 100% minus the forgetting index on the day when the repetition should take place. Here U-Factor is 4377/1463=2.991, and the retrievability is 80.4%. Had the item not been postponed 10 times (see Delay), the retrievability should stand at 90% on the date of repetition as the requested Forgetting index had been set at 10%
- Future repetitions - estimated number of repetitions of the item in the next thirty years, and the time needed for executing repetitions in that period. This value is easily derived from A-Factor, Repetitions, Forgetting index, and the matrix of optimal factors (see: SuperMemo Algorithm). You can click on the Forgetting index field to change the forgetting index and see how that changes the estimation of future repetitions. For topics, the number of presentations depends on A-Factor only. SuperMemo roughly predicts that there will still be 1 repetition of the presented item in the next 30 years. Avg Time in Statistics makes it possible to estimate that the cost of retaining the presented item in memory until 2039 is 9 seconds on the assumption the item will not be forgotten in the meantime. Still, the probability of a memory lapse before 2039, assuming no delays, is 10% (1 repetition with the forgetting index of 10% result in 0.9 probability of correct recall). Note that Future Repetition is the estimate from before the execution of a repetition. After the repetition, the estimate is likely to go to zero, meaning, this item became a part of "permastore" (i.e. it might be remembered till the end of an average life)
- Delay - repetition delay as compared with the optimum date. Due to 10 postpones, the presented item has been delayed by 2259 days resulting in the interval delay quotient of 2.067 (i.e. used interval / optimum interval = 4377/2118 = 2.067). This means that used interval - optimum interval = days of delay (4377-2118=2259).
- Type - type of the element: item, topic or task (see also: Topics vs. items) and its current status: dismissed, pending or memorized. The presented element is an example of a memorized item. Memorized items are color-coded in aqua blue, while memorized topics are lime green
Repetition data (right panel)
To understand repetition parameters displayed on the right of the element data window you may need some rudimentary knowledge of SuperMemo Algorithm. This knowledge is not essential for your progress in learning. Here are the fields of the repetition data in element data window:
- New interval - interval increase displayed as used interval -> new interval. New interval would optimally be equal to Optimal interval; however, two factors may make these two values differ: (1) a degree of interval dispersion is needed to avoid scheduling a large number of repetitions on the same day (this dispersion also speeds up the convergence of the optimization algorithm), and (2) some constraints imposed on the new interval may make it impossible for it to equal Optimum interval. For example, SuperMemo will never set the new interval to be shorter than the old interval (Interval). For a low forgetting index, it is quite common that Optimal interval is shorter than Interval. This is not a reason for worry, but might be an indication that the forgetting index is set too low. Used interval may be greater than Interval if the repetition has been delayed. The interval after the presented repetition will increase from 4377 days (i.e. almost 12 years) to 34 years 7 months and 14 days
- New Priority - new priority of the element in percent and as a position in the priority queue. The priority of items does not change during repetitions. Priority of topics is reduced gradually unless their interval is shortened manually or some incremental reading operations are executed on the topic. This field is color-coded in the same way as Priority. In the picture, the priority of the item has not changed as a result of the repetition
- Repetitions - number of repetitions of the displayed item (including the just-made repetition). If the item had been forgotten, the number of memory lapses is displayed after the colon. The number in the parentheses indicates the number of repetitions that the item would need to reach its current interval assuming the current value of the matrix of optimal factors and no memory lapses on the way (the so called repetition category). This hypothetical value is used to index the matrix of optimal factors and the matrix of retention factors in computing the new values of individual matrix entries at repetitions. The exemplary item in the picture has just been repeated for the 9th time and has not been forgotten yet. In a stable collection with relatively few repetition delays, the repetition category is usually close to the repetition number. Here it is 14.0
- Next repetition - date on which the next repetition should take place and the number of repetitions already scheduled on that day (in parentheses). Next repetition will be scheduled on Oct 19, 2043. There has been no elements scheduled for review on that day.
- Optimum interval - optimum interval the item should use to ensure the forgetting probability determined by Forgetting index. The optimum interval before the next repetition is 34 years 6 months and 28 days. SuperMemo determines that if the item is repeated after that date, the probability of forgetting will surpass 10%
- Expected FI - expected forgetting index derived from the interval (see the description of SuperMemo Algorithm). Due to the longer than optimum interval, the expected forgetting index was 21.4% (i.e. more than the requested forgetting index of 10%)
- Estimated FI - estimated forgetting index derived from the grade scored (see the description of SuperMemo Algorithm). From the grade scored in the present repetition, the estimated forgetting index was computed as 0.2%. This low value indicates that the presented item is doing quite well in repetitions (as determined by a good grade scored)
- New A-Factor - new value of A-Factor estimated for the displayed item after the just-made repetition. A-Factor was increased during the presented repetition from 4.307 to 5.344 (as a result of a good grade and a low Estimated FI)
- New U-Factor - new value of U-Factor (i.e. the quotient of the new interval and the old interval. U-Factor was changed from 2.991 to 2.889. In other words, the present increase in interval is less than the last increase in the interval back in 1997
- Normalized grade - grade normalized for the optimum interval for the forgetting index equal 10% (see the description of SuperMemo Algorithm). Here the normalized grade is 4.40. The numbers in the parentheses shows the minimum and maximum values of the normalized grade computed using four different methods
- R-Factor change - change of the R-Factor corresponding to the current repetition category (the one displayed in parentheses at Repetitions) and A-Factor (displayed at A-Factor among element parameters). See the description of SuperMemo Algorithm for details. In the parentheses, the number of repetition cases used to compute that particular RF matrix entry is displayed. Only grades less than Pass (3) reduce the R-Factor (forgetting pulls the forgetting curve down reducing the interval needed to reach the same forgetting index). The grade did not change the relevant entry of the R-Factor matrix (R-Factor stays at the same level of 4.200). The grade is not visible in the element data window (you can see it at the bottom of the element window) and was Bright (5) in the presented case. That entry can be found in the RF matrix in Analysis as RF[14,4.2] where 14 is a rounded value of the repetition category (14.0), and 4.2 is the lower limit of the A-Factor category (for A-Factor 4.307). 37 repetitions have been executed for repetition category 14 and A-Factor within the [4.2-4.5] range
- O-Factor change - change of the O-Factor corresponding to the current repetition category (the one displayed in parentheses at Repetitions) and A-Factor (displayed at A-Factor among element parameters). See the description of SuperMemo Algorithm for details. In the parentheses, the number of repetition cases used to compute that particular OF matrix entry is displayed. For good grades, O-Factors also increase; however, as they come from smoothing R-Factors, these changes are less prominent. In the presented case, the O-Factor has not changed detectably and stayed at the level of 1.312. 37 repetitions have been executed for repetition category 14 and A-Factor within the [4.2-4.5] range